Sign of a function1 is a modifier of the function's operation which characterizes the function's competence area in terms of quality, distance, direction and scale of information processing.

The competence area of a function is an area where the function operates in accordance with all parameters peculiar to this function. All possible information space of an information element in regard to the concept signs can be described by two areas:

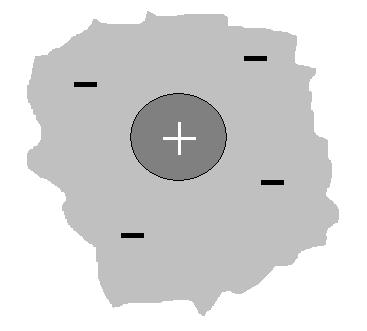
1. The competence area of a "minus" function covers all information space on the information element.
2. The competence area of a "plus" function covers a limited information area of the information element's space.

The “Minus” sign denotes quality of information processing when an IM function is biased as follows:
- in terms of scale — globally, generally; 
- in terms of direction — outwards;
- in terms of distance — both at close anfar ranges; at any psychological distance;
- in terms of quality — both in the positive and negative areas.

The “Plus” sign denotes quality of information processing when an IM function is biased as follows:
- in terms of scale — locally, specifically, in detail;
- in terms of direction — inwards;
- in terms of distance — at close range, at near psychological distance;
- in terms of quality — within the positive area only;

If a function is denoted by the "plus" sign, it means that the function has only a limited ("plus") area of competence and it cannot process the respective "minus" area adequately, in accordance with the function's dimension. Responses of a "plus" function (of any dimension) in the "minus" area are similar to responses of one-dimensional functions. A "plus" function tries to stay away from its incompetence area (the "minus" area), avoiding it in all ways.

Other papers on the topic:
1. Eglit I.M. TIM identification
2. Eglit I.M. Signs of the psychic functions in the A-model

Eglit IM ©